ਘੜੀ ਕੋਣ ਸਮੱਸਿਆ

ਇਸ ਚਿੱਤਰ ਦੇ ਵਿੱਚ ਐਨਾਲਾਗ ਘੜੀ ਦੇ ਹੱਥ ਦੁਆਰਾ 2:20 'ਤੇ ਬਨਾਏ ਜਾ ਰਹੇ ਕੋਣਾਂ ਬਾਰੇ ਪਤਾ ਚਲਦਾ ਹੈ।

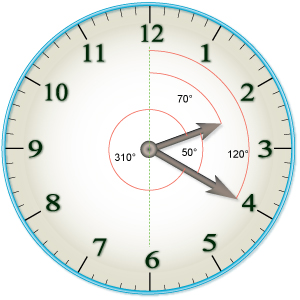
ਘੜੀ ਕੋਣ ਸਮੱਸਿਆ, ਗਣਿਤ ਸਮੱਸਿਆ ਦੀ ਇੱਕ ਕਿਸਮ ਹੈ, ਜਿਸ ਵਿੱਚ ਇੱਕ ਐਨਾਲਾਗ ਘੜੀ ਦੇ ਹੱਥ ਦੇ ਵਿਚਕਾਰ ਕੋਣ ਨੂੰ ਲੱਭਣਾ ਹੁੰਦਾ ਹੈ।

ਗਣਿਤ ਸਮੱਸਿਆ

ਘੜੀ ਕੋਣ ਸਮੱਸਿਆ ਦੇ ਸੰਬੰਧ ਦੋ ਵੱਖ-ਵੱਖ ਨਾਪਾਂ ਨਾਲ ਹਨ: ਕੋਣ ਅਤੇ ਸਮਾਂ। ਕੋਣ ਨੂੰ ਖਾਸ ਤੌਰ 'ਤੇ 12 ਵਜੇ ਦੇ ਨਿਸ਼ਾਨ ਤੋਂ ਡਿਗਰੀ ਵਿੱਚ ਮਾਪਿਆ ਜਾਂਦਾ ਹੈ ਅਤੇ ਸਮਾਂ ਆਮ ਤੌਰ 'ਤੇ 12-ਘੰਟੇ ਘੜੀ ਤੇ ਅਧਾਰਿਤ ਹੁੰਦਾ ਹੈ।

ਅਜਿਹੀ ਸਮੱਸਿਆ ਨੂੰ ਹੱਲ ਕਰਨ ਲਈ ਇੱਕ ਢੰਗ ਹੈ: ਪ੍ਰਤੀ ਮਿੰਟ ਡਿਗਰੀ ਕੋਣ ਦੇ ਤਬਦੀਲੀ ਦੀ ਦਰ ਉੱਤੇ ਵਿਚਾਰ ਕਰਨਾ। ਇੱਕ ਆਮ 12-ਘੰਟੇ ਐਨਾਲਾਗ ਘੜੀ ਦਾ ਘੰਟੇ ਦਾ ਹੱਥ 12 ਘੰਟੇ (720 ਮਿੰਟ) ਵਿੱਚ 360° ਜਾ ਪ੍ਰਤੀ ਮਿੰਟ 0.5° ਦਾ ਕੋਣ ਬਣਾਉਂਦਾ ਹੈ। ਮਿੰਟ ਵਾਲਾ ਹੱਥ 60 ਮਿੰਟਾਂ ਵਿੱਚ 360° ਜਾ ਪ੍ਰਤੀ ਮਿੰਟ 6° ਦਾ ਕੋਣ ਬਣਾਉਂਦਾ ਹੈ।

ਘੰਟੇ ਹੱਥ ਦੇ ਕੋਣ ਲਈ ਸਮੀਕਰਨ

${\theta }_{\text{hr}}=0.5^{\circ }\times M_{\mathrm{\Sigma }}=0.5^{\circ }\times (60\times H+M)$

ਇਥੇ:

• ਫਰਮਾ:Mvar,12 ਵਜੇ ਤੋਂ ਲੈ ਕੇ ਘੰਟੇ ਵਾਲੇ ਹੱਥ ਦੁਆਰਾ ਬਣਾਇਆ ਹੋਇਆ ਕੋਣ ਹੈ।
• ਫਰਮਾ:Mvar ਘੰਟਾ ਹੈ।
• ਫਰਮਾ:Mvar ਘੰਟੇ ਤੋਂ ਬਾਅਦ ਤੈਅ ਕੀਤੇ ਹੋਏ ਮਿੰਟ ਹਨ।
• ਫਰਮਾ:Math 12 ਵਜੇ ਤੋਂ ਲੈ ਕੇ ਤੈਅ ਕੀਤੇ ਹੋਏ ਮਿੰਟ ਹਨ।$M_{\mathrm{\Sigma }}=(60\times H+M)$

ਮਿੰਟ ਹੱਥ ਦੇ ਕੋਣ ਲਈ ਸਮੀਕਰਨ

${\theta }_{\text{min.}}=6^{\circ }\times M$

ਇਥੇ:

• ਫਰਮਾ:Mvar 12 ਵਜੇ ਤੋਂ ਲੈ ਕੇ ਮਿੰਟ ਵਾਲੇ ਹੱਥ ਦੁਆਰਾ ਬਣਾਇਆ ਹੋਇਆ ਕੋਣ ਹੈ।
• ਫਰਮਾ:Mvar ਮਿੰਟ ਹਨ।

ਉਦਾਹਰਨ

ਮੰਨ ਲਓ ਕਿ ਸਮਾਂ 5:24 ਹੈ। ਤਾਂ ਫਿਰ ਮਿੰਟ ਵਾਲੇ ਹੱਥ ਦੁਆਰਾ ਬਣਾਇਆ ਹੋਇਆ ਕੋਣ ਇਸ ਤਰਾਂ ਪਤਾ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ:

${\theta }_{\text{hr}}=0.5^{\circ }\times (60\times 5+24)=162^{\circ }$

ਮਿੰਟ ਵਾਲੇ ਹੱਥ ਦੁਆਰਾ ਬਣਾਇਆ ਹੋਇਆ ਕੋਣ:

${\theta }_{\text{min.}}=6^{\circ }\times 24=144^{\circ }$

ਘੜੀ ਦੇ ਹੱਥਾਂ ਦੇ ਵਿਚਕਾਰ ਕੋਣ ਲਈ ਸਮੀਕਰਨ

ਘੜੀ ਦੇ ਹੱਥਾਂ ਦੇ ਵਿਚਕਾਰ ਕੋਣ ਪਤਾ ਕਰਨ ਲਈ ਇਹ ਫ਼ਾਰ੍ਮੂਲਾ ਵਰਤਿਆ ਜਾ ਸਕਦਾ ਹੈ:

$\begin{array}{cc}\mathrm{\Delta }\theta & =|{\theta }_{\text{hr}}-{\theta }_{\text{min.}}|\\ & =|0.5^{\circ }\times (60\times H+M)-6^{\circ }\times M|\\ & =|0.5^{\circ }\times (60\times H+M)-0.5^{\circ }\times 12\times M|\\ & =|0.5^{\circ }\times (60\times H-11\times M)|\\ \end{array}$

ਇਥੇ:

• ਫਰਮਾ:Mvar, ਘੰਟੇ ਹਨ।
• ਫਰਮਾ:Mvar, ਮਿੰਟ ਹਨ।

ਜੇਕਰ ਕੋਣ 180 ਡਿਗਰੀ ਤੋਂ ਵੱਧ ਹੁੰਦਾ ਹੈ ਤਾਂ ਫਿਰ ਇਸਨੂੰ 360 ਡਿਗਰੀ ਦੇ ਵਿਚੋਂ ਘਟਾ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ।

ਉਦਾਹਰਨ 1

ਮੰਨ ਲਓ ਕਿ ਸਮਾਂ 2:20 ਹੈ:

$\begin{array}{cc}\mathrm{\Delta }\theta & =|0.5^{\circ }\times (60\times 2-11\times 20)|\\ & =|0.5^{\circ }\times (120-220)|\\ & =50^{\circ }\end{array}$

ਉਦਾਹਰਨ 2

ਮੰਨ ਲਓ ਕਿ ਸਮਾਂ 10:16 ਹੈ।

$\begin{array}{cc}\mathrm{\Delta }\theta & =|0.5^{\circ }\times (60\times 10-11\times 16)|\\ & =|0.5^{\circ }\times (600-176)|\\ & =212^{\circ }(>180^{\circ })\\ & =360^{\circ }-212^{\circ }\\ & =148^{\circ }\end{array}$

ਇੱਕ ਘੜੀ ਦੇ ਘੰਟੇ ਅਤੇ ਮਿੰਟ ਹੱਥ ਇੱਕੋ ਜਗਹ 'ਤੇ ਕਦੋਂ ਹੁੰਦੇ ਹਨ?

ਇੱਕ ਘੜੀ ਦੇ ਘੰਟੇ ਅਤੇ ਮਿੰਟ ਹੱਥ ਇੱਕੋ ਜਗਹ 'ਤੇ ਉਦੋਂ ਹੁੰਦੇ ਜਦੋਂ ਉਹਨਾਂ ਦਾ ਕੋਣ ਸਮਾਨ ਹੋਵੇ।

$\begin{array}{cc}{\theta }_{\text{min}}& ={\theta }_{\text{hr}}\\ \Rightarrow 6^{\circ }\times M& =0.5^{\circ }\times (60\times H+M)\\ \Rightarrow 12\times M& =60\times H+M\\ \Rightarrow 11\times M& =60\times H\\ \Rightarrow M& =\frac{60}{11}\times H\\ \Rightarrow M& =5.\overline{45}\times H\end{array}$

ਫਰਮਾ:Mvar ਸੀਮਾ 0-11 ਵਿੱਚ ਇੱਕ ਪੂਰਨ ਅੰਕ ਹੈ। ਇਹ ਸਾਨੂੰ ਕੁਝ ਇਸ ਤਰਾਂ ਦੇ ਸਮੇਂ ਦਿੰਦਾ ਹੈ: 0:00, 1:05.ਫਰਮਾ:Overline, 2:10.ਫਰਮਾ:Overline, 3:16.ਫਰਮਾ:Overline, 4:21.ਫਰਮਾ:Overline, 5:27.ਫਰਮਾ:Overline. 6:32.ਫਰਮਾ:Overline, 7:38.ਫਰਮਾ:Overline, 8:43.ਫਰਮਾ:Overline, 9:49.ਫਰਮਾ:Overline, 10:54.ਫਰਮਾ:Overline, ਅਤੇ 12:00. (0.ਫਰਮਾ:Overline ਮਿੰਟ ਬਿਲਕੁਲ 27 ਹਨ। ਫਰਮਾ:Overline ਸਕਿੰਟ)

ਇਹ ਵੀ ਵੇਖੋ

• ਘੜੀ ਸਥਿਤੀ

ਬਾਹਰੀ ਜੋੜ

• http://www.delphiforfun.org/Programs/clock_angle.htm ਫਰਮਾ:Webarchive
• http://www.ldlewis.com/hospital_clock/ - extensive clock angle analysis
• http://www.jimloy.com/puzz/clock1.htm ਫਰਮਾ:Webarchive